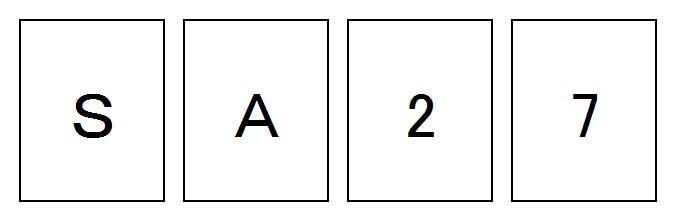
表にはアルファベット、裏には数字が書かれている4枚のカードがあります。
このカードには「母音の裏には偶数が書かれていなければならない」というルールがあります。
このルールが成立しているかどうかを確かめるには、どのカードをめくる必要があるでしょうか?
直感で答えると間違いやすい問題の一つ。
Aのみ、もしくはAと2と答える方が多いようです。
Aをめくらなくてはならないのは、わかりやすいでしょう。
Aの裏が偶数でなく奇数だったらルールに反しているので。
しかし、2の裏にはどんなカードが書かれていてもルール違反にはなりません。
「母音の裏に偶数が書かれている」必要はありますが、「偶数の裏に母音が書かれている」必要はないのです。
よって正解はAと7をめくることです。
7の裏が母音であった場合は、ルールが成立していないということになるからです。

「PならばQ」という命題があるとき、「QでないならPではない」という命題を対偶といいます。
もとの命題が真であれば、対偶問題も必ず真です。
逆に対偶が真であれば、もとの命題も真となります。
4枚カード問題は、形式論理学でいう待遇に関する規則を当てはめれば、簡単に解くことができます。
「表が母音ならば裏は偶数」の対偶は「裏が偶数でない(奇数)ならば表は母音ではない」となります。
ですから、裏が偶数でない7のカードをめくって、表が母音でないことを確認する必要があるのです。
どうやら私たちは4枚カード問題のように、日常生活ではあまりお目にかからない論理学の形式に沿った推論は苦手なようです。
この問題はウィンソンという心理学者によって考えられました。
様々な人物を対象に多くの実験が行われましたが、正解率は10%にも満たないことがほとんどだったようです。
しかしこの問題を少し変えて、日常生活に関わりのあるような内容にすると正解率は一気に上がるといわれています。
広告