【問題】
目の前に3枚のパネルがあり、1枚は当たりで2枚はハズレ。
あなたがパネルを選択すると、コンピューターが残り2枚のパネルのうちの1枚を自動的に開きます。
その時に開かれるパネルは必ずハズレです。
ここであなたは最初に選択したパネルを、まだ開かれていないもう1枚のパネルに変更する権利を与えられます。
さて、あなたはパネルを変更するべきでしょうか？
この問題はアメリカの人気番組の中で実際に行われていたゲームとほぼ同じ内容で、司会者の名前をとってモンティ・ホール問題と呼ばれています。
1997年に世界最高のＩＱ228の持ち主であるマリリン・ヴォス・サバァントが掲載している「マリリンに聞いてみよう」というコラムで話題になり、多くの数学者や経済学者の間でも物議を醸した有名な確率の問題です。
この問題では多くの人が「パネルを変更しない」と答えます。
今の時点で残ったパネル2枚のうち、1枚は当たりで1枚はハズレ。
つまり、当たる確率は2分の1だから、変更してもしなくても変わらないと考えるわけです。
変更してハズレを引いた方が、悔しい気もしますしね。
しかしこの問題のケースでは、選択を変えた方が有利になります。
3分の1から3分の2へと、当たる確率は2倍になるのです。
なんだか狐につつまれた感じがする方もいるでしょうから、表を用いて説明します。
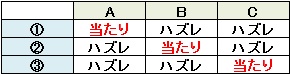
起こり得るケースは①～③のどれかなので、最初の選択で当たりを引く確率（事前確率）は3分の1です。
仮にあなたが最初にＡを選んだとしましょう。
①の場合
Ａが当たりなので、パネルの選択を変更するとハズレてしまいます。
②の場合
コンピューターが開くのは必ずハズレのCなので、パネルの選択をAからBに変更すれば当たりです。
③の場合
コンピューターが開くのは必ずハズレのBなので、パネルの選択をAからCに変更すれば当たりです。
3通りのうち、変更するとハズレてしまうのは1通り。変更すれば当たりになるのは2通り。
つまり変更しないと当たる確率は3分の1のままで、変更すれば当たる確率は3分の2になります。
この問題で重要なポイントは、コンピューターが残り2枚のパネルのうちから「必ずハズレのパネルを1枚開く」ということです。
この条件が崩れてしまうとモンティ・ホール問題はなりたちません。
コンピューターがパネルを開かなかったり、純粋にランダムで選ぶ（当たりのパネルを選んでしまう可能性がある）場合は、問題の前提が変わってしまいます。
モンティ・ホール問題は、直感で選んだ答えと理論値のズレを示す代表的な事例です。
では、直感的にも判断できるようにパネルを100枚にして考えてみましょう。
まずあなたは100枚のパネルの中から1枚を選びます。
この時点では、当たりを引く確率は100分の1です。
次にコンピューターが残り99枚のパネルのうちの98枚のハズレを開きます。
残ったパネルはあなたが最初に勘で選んだパネルと、「必ずハズレを開くコンピューターが99枚のうちでただ1枚選ばなかったパネル」です。
さて、どっちのパネルの方が当たりの確率が高いでしょうか？
これは直感的にも判断しやすいと思います。
このように確率がわかりにくいときは、極端な値にすると分かりやすくなる場合があります。
広告
「モンティ・ホール問題」への161件のフィードバック
コメントは停止中です。