※画像をクリックすると拡大します
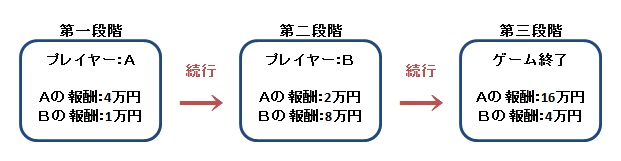
これはゲーム理論で登場するムカデゲームを少し変えたものです。（通常は第五段階までゲームは行われる）
ゲームのルールを説明すると、まずプレイヤーＡが「終了」か「続行」を選択します。
もし終了を選択すれば、プレイヤーＡに報酬が4万円、プレイヤーＢに報酬が1万円与えられてゲームは終わります。
しかし続行を選択した場合は、プレイヤーＢに順番が変わり、同じように「終了」か「続行」の選択が行われます。
ここでもＢが続行を選択すれば、プレイヤーＡに報酬が16万円、プレイヤーＢに報酬が4万円与えられゲームは終了するのですが…
プレイヤーＡ、Ｂがお互い相手の戦略をもとに最適な行動を取った場合。
つまり合理性に基づいて自分の利益だけを追求した場合、このゲームはどこで終了するでしょうか？
プレイヤーＡ、Ｂは協力関係を持たない赤の他人で、ゲーム終了後に報酬を分配するなどの打ち合わせはできないものとします。
最初に選択を行うプレイヤーＡの立場として考えてみましょう。
プレイヤーＡにとって一番望ましいのは、第三段階まで行き16万円の報酬をもらえることです。
しかし第二段階の時点で、プレイヤーＢに終了されてしまうと推論できます。
なぜならプレイヤーＢは第二段階の時点で終了すれば8万円もらえますが、続行してしまうと報酬が4万円に減ってしまうからです。
第二段階でゲームが終了するとプレイヤーＡの報酬は2万円ですが、第一段階で終了させれば4万円もらうことができます。
ですからプレイヤーＡは第一段階で終了を選択します。
したがってプレイヤーＡが4万円、プレイヤーＢが1万円の報酬を受け取りゲームは終了となります。
このようにスタートからではなく、ゴールからスタートに向かっていく推論方法を「後ろ向き帰納法」といいます。
この問題は理屈の上では納得いくかもしれませんが、多くの方がしっくりこないでしょう。
第三段階までいけば4倍の報酬がもらえるのにもかかわらず、第一段階でゲームが終了してしまうからです。
このようにすべてのプレイヤーが相手の戦略をもとに、自己の利益を最大化しようとしたときに起こる均衡状態を「ナッシュの均衡」といいます。
ナッシュの均衡はゲーム理論の基礎となるもので、囚人のジレンマがもっとも有名な例です。
実際にムカデゲームを五段階で実験してみた結果、最後の段階まで続行したプレイヤーはわずか5％だったそうです。
広告
「ムカデゲーム｜ナッシュ均衡」への152件のフィードバック
コメントは停止中です。